Explanation
Tables of Minimum Eigen Values
Computer Program,
R Code
Introduction
Technical Considerations
Example
Parallel Analysis is a procedure sometimes used to determine the number of
Factors or Principal Components to retain in the initial stage of Exploratory Factor Analysis.
This discussion assumes that the user understands Factor Analysis and the
procedure of Principal Component extraction, and no details for these are provided here.
A critical decision in Exploratory Factor Analysis is to determine how many Principal
Components to retain, as each extraction produces decreasingly significant Factors.
Retaining too few leads to a loss of information in the data, and retaining too many
includes trivial and random information. Both of these produce misleading and unreproducible results.
Traditionally, researchers depend on one or more of the following criteria to
determine how many components to retain.
- The most common, and the default criteria in most statistical packages
is the K1 rule. Principal Components are retained while the Eigen Value
(the Variance associated with the component), is >=1. This is based on
the argument that, in a correlation matrix, each variable contribute a
variance of 1, so a component that accounts for less than that has no meaning and should
be discarded. The criticism to the K1 rule is that the Eigen values are inflated by random associations
in the data, so that the use of the K1 rule often retains more components or factors than appropriate,
particularly when the sample size is small.
- Another rule is using the Scree Test. The Eigen values are plotting against
component number, and when the sharp decrease in Eigen values level off (the scree),
the remaining components are abandoned. This is based on the arguments that the initial and
significant components each extracts a large proportion of the variance from the correlation matrix,
while the insignificant ones contain mostly data noise and so their Eigen values are similar. The criticism
of using the Scree Test is that it depends on eye balling when there is no sharp transition where the scree begins.
Thus researchers often disagree where the scree begins.
- Some researchers tried different retention levels, and match the results with
the theoretical model of the data. This does produce neat outcomes, but
runs the risk that, if the underlying theory is flawed to start with, then the results tend not to be reproducible.
Parallel Analysis takes a different approach, and is based on the Monte Carlo simulation.
A data set of random numbers, but having the same sample size and number of variables as the user's
research data, are subjected to analysis, and the Eigen values obtained are recorded. This is repeated
many times (often between 50 and 100 iterations, and the tables later on this page used 1000 iterations).
The mean and Standard Deviation of the replicated Eigen values for each component are then calculate, from which
the 95th percentile value is obtained (95th percentile = mean + 1.64SD). These form
the standard against which the Eigen value of each component from the research data is compared, and a components
is retained if its Eigen value exceeds the 95th percentile of the simulated values. The argument being
that a component should be retained if its Eigen value is clearly greater (at 95th percentile) than that
obtained at random.
References
Hayton JC, Allen DG and Scarpello V (2004)Factor Retention Decisions in Exploratory
Factor Analysis: a Tutorial on Parallel Analysis. Organizational Research Methods 2004; 7; 191
Watkins MW (2006)Determining Parallel Analysis Criteria.
Journal of Modern Applied Statistical Methods Vol. 5, No. 2, 344-346
Free program to do Parallel Analysis from someone else downloadable from WWW
Ledesma RD (2007)Determining the Number of Factors to Retain in EFA: an easy-to-use
computer program for carrying out Parallel Analysis. Practical Assessment, Research, and
Evaluation Volume 12, Number 2, p. 1-11 Accesible on www.
Word file with SPSS commands for Parallel Analysis
Press WH, Flannery VP, Teukolsky SA, Vetterling WT (1989). Numerical Recipes in Pascal.
Cambridge University Press IBSN 0-521-37516-9 p.395-396 and p.402-404. (computer program to
extract Eigen Values and Vectors from a correlation matrix using the Jacobi algorithm).
Monte Carlo simulation models the statistical process, but uses randomly generated numbers. The
calculations are replicated numerous time to produce a standard based on random numbers, against which
research data and results can be compared.
For an adequate simulation, numerous iterations may be necessary. When the calculations involve iterations
and matrix manipulations, the memory requirement and computing time may exceed that allowable from a server.
For example, a parallel analysis for 40 variables, a sample size of more than 50, and attempting 50 replication,
will exceed the 30 seconds of computing time usually allowable by a php server, causing the program to crash.
Resources for Parallel Analysis on this page therefore exists in two forms. These are :
- Tables of critical Eigen values for Factor Analysis of 4 to 100 variables, over a range of commonly used sample
sizes, and obtained over 1000 replications of simulation for each.
- A small Javascript program to carry out a specific Parallel Analysis, if requirements are not met by the tables.
The algorithm used for resources on this page is from that published in Numerical Recipes for Pascal,
translated to Javascript. Please note that, as with any Monte Carlo simulation, each run uses different sets
of random numbers, so the results are closely similar but not the same. Users should therefore not be alarmed
by minor differences in the output.
Simulations on this page use computer generated random numbers that are normally distributed, with mean of 0 and SD of 1.
Although this is usually acceptable, and the results differ little from any other methods of generating random numbers,
it is different to the strict requirements of Parallel Analysis.
- Strictly, each variable in the simulation should mimic the real data. Normally distributed random numbers
should only be used for those variables that are normally distributed. For measurements such as Likert Scale,
the random number should be integers randomised to values between 1 and 5 without a defined distribution. For
binary variables (female/male, alive/dead, no/yes), the number should be randomised between 0 and 1.
- To comply with the strict requirements of Parallel Analysis therefore, the random dataset needs to be customised
to the nature of each of the variables in the research data. To use normally distributed random numbers for all variables, such as
that in the programs of this page, the user needs to accept the argument that the difference thus created will be
trivial and unlikely to affect the decision on how many components to retain. Users should be aware that this
argument is accepted by many, but not all, amongst those who are authoritative in these matters.
There are many papers discussing Parallel Analysis and some free software that are available on the www.
I have put links to two downloadable software in the introduction panel for users who wish to have a desk top
programs for this. I have neither downloaded nor evaluate these programs myself, so the user should evaluate these
packages for himself/herself.
The tables and programs on this page are for Principal Components only, where the diagonals of the correlation matrix
are all 1s, and not Principal Factor Analysis, where the diagonals of the correlation matrix is replaced with estimates
of communalities. The results are not appropriate for the latter model.
This section demonstrate how Parallel Analysis can be used instead of the K1 rule to determine the number of factors to retain. This consists of the following steps.
- Using the researcher's data, an initial Principal Component Analysis is carried out, but overriding the K1 rule,
so that the number of components retained is the same as the number of variables. This will include
the full array of Eigen values, usually in order of magnitude.
- Either looking up the tables on this page, or using the Javascript program, the standards (minimum Eigen values for
component retention) are determined by Parallel Analysis.
- The Eigen values from the research data are compared with the Standards. The components to retained are those where
the Eigen values from the research data exceeds both 1 (K1 rule), and the standard value from Parallel Analysis.
- The rest of the Factor Analysis is then calculated using only the number of components that are retained. If statistical
packages such as SPSS or SAS is used, the program is configured to extract the appropriate number of components.
Example
The following example demonstrate the procedures. The data are the default example data from the FactorAnalysis.php. Please note that this is only an example using a small sample of computer generated random numbers, a Factor Analysis with 6 variables will need a sample size much greater than 25 cases to have any reproducibility at all.
| 0.66 | 0.23 | 0.28 | 0.12 | 0.24 |
| 0.66 | | 0.23 | 0.05 | 0.23 | 0.36 |
| 0.23 | 0.23 | | 0.66 | 0.26 | 0.23 |
| 0.28 | 0.05 | 0.66 | | 0.39 | 0.31 |
| 0.12 | 0.23 | 0.26 | 0.39 | | 0.76 |
| 0.24 | 0.36 | 0.23 | 0.31 | 0.76 | |
We wish to conduct a Factor Analysis on a data set, which has 6 variables, and a sample size of 25.
The correlation matrix for this set of data is as shown in the table to the left.
Step 1 : Initial extraction of all possible components (First Run)
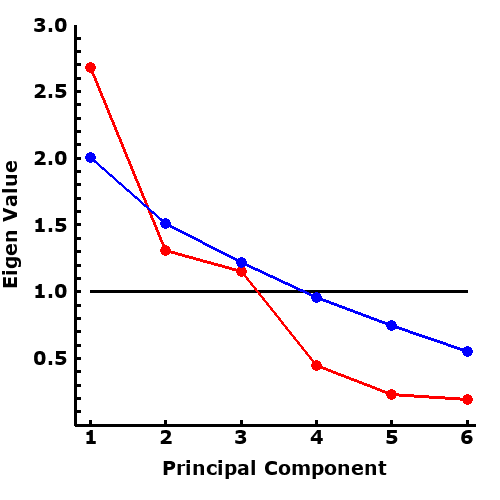
The original data or the correlation matrix can be initially analysed, to examine the Eigen values. In order of scale, they are 2.68, 1.31, 1.15, 0.45, 0.23, 0.19. These are shown (in red) in the plot to the right.
Step 2 : Parallel Analysis
The parameter for this example are number of variables=6, and sample size=25, the same as that
from the research data. Please note: only 100 iterations are performed in this example. In a real analysis, iterations of 500-1000 are used to ensure the results are robust and reproducible to the third decimal point. The results of the Parallel Analysis show that the upper 95% confidence of Eigen Values are 2.01, 1.51, 1.22, 0.96, 0.75, 0.55, as shown in blue in the plot to the right.
Step 3 : Decisions
The plot to the right demonstrate the various methods of decision making.
- The Scree test is performed by eyeballing the Eigen values from the data (red line). It can be seen that the Eigen Values decrease rapidly in the first 4 Principal Components before they flattened out. According to the Scree Test therefore, 4 factors should be retained
- Comparing the Eigen values from the data (red line) against K1 rule of 1 (black horizontal line), 3 Eigen values exceeded the value of 1, According to the K1 rule therefore, 3 factors should be retained
- Comparing the Eigen values from the data (red line) against those estimated from Parallel Analysis (blue line), only the first Eigen value exceeded that from Parallel Analysis. Accordingly, only one factor should be retained.
These results demonstrate how both the Scree and K1 Test may include excessive number of factors. The scree test is the least robust, as it depends on human judgement, so will vary widely. The K1 test extracts too many factors because it takes into consideration all correlations in the data, even if they occur randomly. Parallel analysis, by using Monte Carlo simulation, is the most robust of the three. the results in this example is not surprising, as the example data consists of computer generated random numbers, with no significant inherent correlations between the variables.
Step 4 : Second and Final Run
Once the number of factors to be retained is determined (by whichever method chosen), The Factor Analysis can be performed again, with the number of factors to be retained specified
Explanation
4-9 Variables
10-20 Variables
25-50 Variables
60 Variables
70 Variables
80 Variables
90 Variables
100 Variables
The tables show critical Eigen values for retention of a factor. Each table provides values for
Factor Analysis with a particular number of variables. The columns are the sample size of the research data,
and the rows are factor numbers (in order of size). Each cell contains the critical minimum Eigen value, which the
Eigen value of that factor must exceed if it is to be retained. Where there is no value provided, the K1 rule
(Eigen value >=1.0) should be used.
These critical numbers are obtained using data that are normally distributed random numbers to create the
correlation matrix of the appropriate number of variables, and repeated 1000 iterations. The numbers represents the
95th percentile of the Eigen values so obtained for each factor.
The tables contains only those Eigen values that are >1, as factors with Eigen values of less than 1 are usually not retained.
| SSiz | 20 | 40 | 60 | 80 | 100 | 150 | 200 | 300 | 400 | 500 |
| Number of variables = 4 |
| f1 | 1.81 | 1.58 | 1.46 | 1.39 | 1.36 | 1.29 | 1.25 | 1.20 | 1.17 | 1.16 |
| f2 | 1.30 | 1.21 | 1.17 | 1.15 | 1.14 | 1.11 | 1.10 | 1.08 | 1.07 | 1.06 |
| f3 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 |
| Number of variables = 5 |
| f1 | 2.01 | 1.67 | 1.53 | 1.47 | 1.41 | 1.34 | 1.29 | 1.24 | 1.20 | 1.18 |
| f2 | 1.47 | 1.32 | 1.26 | 1.23 | 1.20 | 1.17 | 1.15 | 1.12 | 1.10 | 1.09 |
| f3 | 1.12 | 1.10 | 1.08 | 1.07 | 1.06 | 1.05 | 1.04 | 1.04 | 1.03 | 1.03 |
| Number of variables = 6 |
| f1 | 2.14 | 1.78 | 1.63 | 1.54 | 1.47 | 1.38 | 1.33 | 1.27 | 1.23 | 1.20 |
| f2 | 1.60 | 1.41 | 1.34 | 1.30 | 1.26 | 1.22 | 1.19 | 1.15 | 1.13 | 1.12 |
| f3 | 1.24 | 1.17 | 1.15 | 1.13 | 1.12 | 1.10 | 1.08 | 1.07 | 1.06 | 1.05 |
| f4 | | 1.00 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 |
| Number of variables = 7 |
| f1 | 2.3 | 1.88 | 1.70 | 1.6 | 1.53 | 1.43 | 1.37 | 1.3 | 1.25 | 1.22 |
| f2 | 1.72 | 1.51 | 1.42 | 1.35 | 1.32 | 1.26 | 1.23 | 1.18 | 1.16 | 1.14 |
| f3 | 1.36 | 1.26 | 1.22 | 1.19 | 1.17 | 1.14 | 1.12 | 1.10 | 1.09 | 1.08 |
| f4 | 1.09 | 1.08 | 1.07 | 1.06 | 1.06 | 1.05 | 1.05 | 1.04 | 1.03 | 1.03 |
| Number of variables = 8 |
| f1 | 2.46 | 1.96 | 1.77 | 1.66 | 1.58 | 1.47 | 1.41 | 1.33 | 1.28 | 1.25 |
| f2 | 1.87 | 1.59 | 1.48 | 1.41 | 1.37 | 1.30 | 1.26 | 1.21 | 1.18 | 1.16 |
| f3 | 1.47 | 1.35 | 1.29 | 1.25 | 1.22 | 1.18 | 1.16 | 1.13 | 1.11 | 1.10 |
| f4 | 1.18 | 1.15 | 1.13 | 1.11 | 1.10 | 1.09 | 1.08 | 1.06 | 1.05 | 1.05 |
| f5 | | | | | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 |
| Number of variables = 9 |
| f1 | 2.59 | 2.06 | 1.83 | 1.7 | 1.64 | 1.51 | 1.43 | 1.35 | 1.3 | 1.27 |
| f2 | 1.97 | 1.67 | 1.54 | 1.47 | 1.42 | 1.34 | 1.29 | 1.23 | 1.2 | 1.18 |
| f3 | 1.59 | 1.42 | 1.34 | 1.30 | 1.27 | 1.22 | 1.19 | 1.16 | 1.13 | 1.12 |
| f4 | 1.29 | 1.22 | 1.19 | 1.17 | 1.15 | 1.13 | 1.11 | 1.09 | 1.08 | 1.07 |
| f5 | 1.05 | 1.05 | 1.06 | 1.05 | 1.05 | 1.04 | 1.04 | 1.03 | 1.03 | 1.03 |
| SSiz | 50 | 75 | 100 | 200 | 300 | 400 | 500 | 600 | 800 | 1000 |
| Number of variables = 10 |
| f1 | 1.99 | 1.79 | 1.68 | 1.46 | 1.38 | 1.32 | 1.29 | 1.26 | 1.23 | 1.20 |
| f2 | 1.66 | 1.53 | 1.47 | 1.32 | 1.26 | 1.22 | 1.20 | 1.18 | 1.16 | 1.14 |
| f3 | 1.44 | 1.37 | 1.32 | 1.22 | 1.18 | 1.16 | 1.14 | 1.13 | 1.11 | 1.10 |
| f4 | 1.26 | 1.22 | 1.19 | 1.14 | 1.11 | 1.10 | 1.09 | 1.08 | 1.07 | 1.06 |
| f5 | 1.11 | 1.10 | 1.09 | 1.07 | 1.06 | 1.05 | 1.04 | 1.04 | 1.04 | 1.03 |
| | | | | | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 |
| Number of variables = 12 |
| f1 | 2.13 | 1.90 | 1.76 | 1.52 | 1.42 | 1.36 | 1.32 | 1.29 | 1.25 | 1.22 |
| f2 | 1.79 | 1.64 | 1.55 | 1.38 | 1.30 | 1.26 | 1.23 | 1.22 | 1.18 | 1.17 |
| f3 | 1.57 | 1.46 | 1.40 | 1.28 | 1.23 | 1.20 | 1.18 | 1.16 | 1.14 | 1.12 |
| f4 | 1.38 | 1.32 | 1.28 | 1.20 | 1.16 | 1.14 | 1.13 | 1.12 | 1.10 | 1.09 |
| f5 | 1.23 | 1.20 | 1.17 | 1.13 | 1.10 | 1.09 | 1.08 | 1.08 | 1.07 | 1.06 |
| f6 | 1.09 | 1.08 | 1.08 | 1.06 | 1.05 | 1.05 | 1.04 | 1.04 | 1.03 | 1.03 |
| SSiz | 50 | 75 | 100 | 200 | 300 | 400 | 500 | 600 | 800 | 1000 |
| Number of variables = 14 |
| f1 | 2.25 | 2.00 | 1.85 | 1.57 | 1.46 | 1.39 | 1.35 | 1.32 | 1.27 | 1.24 |
| f2 | 1.91 | 1.73 | 1.62 | 1.43 | 1.34 | 1.30 | 1.26 | 1.24 | 1.21 | 1.19 |
| f3 | 1.67 | 1.55 | 1.47 | 1.33 | 1.27 | 1.24 | 1.21 | 1.19 | 1.16 | 1.15 |
| f4 | 1.49 | 1.40 | 1.35 | 1.25 | 1.20 | 1.18 | 1.16 | 1.15 | 1.13 | 1.11 |
| f5 | 1.34 | 1.28 | 1.25 | 1.18 | 1.15 | 1.13 | 1.12 | 1.11 | 1.09 | 1.08 |
| f6 | 1.20 | 1.17 | 1.15 | 1.12 | 1.10 | 1.08 | 1.08 | 1.07 | 1.06 | 1.06 |
| f7 | 1.07 | 1.07 | 1.07 | 1.06 | 1.05 | 1.04 | 1.04 | 1.04 | 1.03 | 1.03 |
| Number of variables = 16 |
| f1 | 2.38 | 2.07 | 1.91 | 1.62 | 1.50 | 1.42 | 1.38 | 1.34 | 1.30 | 1.26 |
| f2 | 2.03 | 1.81 | 1.69 | 1.48 | 1.39 | 1.33 | 1.29 | 1.27 | 1.23 | 1.20 |
| f3 | 1.79 | 1.63 | 1.54 | 1.38 | 1.31 | 1.27 | 1.24 | 1.22 | 1.19 | 1.17 |
| f4 | 1.60 | 1.49 | 1.42 | 1.30 | 1.24 | 1.21 | 1.19 | 1.17 | 1.15 | 1.13 |
| f5 | 1.44 | 1.36 | 1.32 | 1.23 | 1.19 | 1.16 | 1.15 | 1.13 | 1.12 | 1.10 |
| f6 | 1.30 | 1.25 | 1.23 | 1.16 | 1.14 | 1.12 | 1.11 | 1.10 | 1.08 | 1.08 |
| f7 | 1.17 | 1.15 | 1.14 | 1.11 | 1.09 | 1.08 | 1.07 | 1.07 | 1.06 | 1.05 |
| f8 | 1.05 | 1.05 | 1.06 | 1.05 | 1.04 | 1.04 | 1.04 | 1.03 | 1.03 | 1.03 |
| SSiz | 50 | 75 | 100 | 200 | 300 | 400 | 500 | 600 | 800 | 1000 |
| Number of variables = 18 |
| f1 | 2.49 | 2.17 | 1.99 | 1.67 | 1.53 | 1.46 | 1.40 | 1.36 | 1.31 | 1.28 |
| f2 | 2.14 | 1.90 | 1.77 | 1.52 | 1.42 | 1.36 | 1.32 | 1.29 | 1.25 | 1.22 |
| f3 | 1.88 | 1.71 | 1.61 | 1.43 | 1.34 | 1.30 | 1.27 | 1.24 | 1.21 | 1.19 |
| f4 | 1.70 | 1.57 | 1.49 | 1.34 | 1.28 | 1.24 | 1.22 | 1.20 | 1.17 | 1.15 |
| f5 | 1.53 | 1.44 | 1.38 | 1.27 | 1.23 | 1.19 | 1.18 | 1.16 | 1.14 | 1.12 |
| f6 | 1.39 | 1.33 | 1.29 | 1.21 | 1.17 | 1.15 | 1.14 | 1.12 | 1.11 | 1.10 |
| f7 | 1.26 | 1.23 | 1.20 | 1.15 | 1.13 | 1.11 | 1.10 | 1.09 | 1.08 | 1.07 |
| f8 | 1.14 | 1.13 | 1.12 | 1.10 | 1.08 | 1.07 | 1.06 | 1.06 | 1.05 | 1.05 |
| f9 | 1.03 | 1.04 | 1.05 | 1.04 | 1.04 | 1.03 | 1.03 | 1.03 | 1.03 | 1.02 |
| Number of variables = 20 |
| f1 | 2.59 | 2.24 | 2.06 | 1.72 | 1.57 | 1.49 | 1.43 | 1.39 | 1.33 | 1.30 |
| f2 | 2.24 | 1.98 | 1.83 | 1.57 | 1.46 | 1.39 | 1.35 | 1.32 | 1.27 | 1.24 |
| f3 | 1.99 | 1.79 | 1.68 | 1.47 | 1.38 | 1.33 | 1.29 | 1.27 | 1.23 | 1.21 |
| f4 | 1.80 | 1.65 | 1.56 | 1.39 | 1.32 | 1.27 | 1.25 | 1.23 | 1.19 | 1.17 |
| f5 | 1.63 | 1.52 | 1.45 | 1.32 | 1.26 | 1.23 | 1.20 | 1.19 | 1.16 | 1.14 |
| f6 | 1.48 | 1.40 | 1.35 | 1.26 | 1.21 | 1.18 | 1.16 | 1.15 | 1.13 | 1.12 |
| f7 | 1.35 | 1.30 | 1.27 | 1.20 | 1.16 | 1.14 | 1.13 | 1.12 | 1.10 | 1.09 |
| f8 | 1.23 | 1.20 | 1.19 | 1.14 | 1.12 | 1.10 | 1.09 | 1.09 | 1.08 | 1.07 |
| f9 | 1.12 | 1.12 | 1.11 | 1.08 | 1.07 | 1.07 | 1.06 | 1.06 | 1.05 | 1.05 |
| f10 | 1.01 | 1.03 | 1.04 | 1.04 | 1.03 | 1.03 | 1.03 | 1.03 | 1.03 | 1.02 |
| SSiz | 100 | 200 | 300 | 400 | 500 | 600 | 800 | 1000 | 1500 | 2000 |
| Number of variables = 25 |
| f1 | 2.22 | 1.82 | 1.65 | 1.56 | 1.49 | 1.44 | 1.38 | 1.34 | 1.27 | 1.23 |
| f2 | 2.00 | 1.67 | 1.54 | 1.46 | 1.41 | 1.37 | 1.32 | 1.28 | 1.23 | 1.20 |
| f3 | 1.84 | 1.57 | 1.46 | 1.40 | 1.35 | 1.32 | 1.28 | 1.25 | 1.20 | 1.17 |
| f4 | 1.71 | 1.49 | 1.40 | 1.34 | 1.30 | 1.28 | 1.24 | 1.22 | 1.17 | 1.15 |
| f5 | 1.60 | 1.42 | 1.34 | 1.30 | 1.26 | 1.24 | 1.21 | 1.19 | 1.15 | 1.13 |
| f6 | 1.50 | 1.36 | 1.29 | 1.25 | 1.22 | 1.20 | 1.18 | 1.16 | 1.13 | 1.11 |
| f7 | 1.41 | 1.30 | 1.24 | 1.21 | 1.19 | 1.17 | 1.15 | 1.13 | 1.11 | 1.10 |
| f8 | 1.32 | 1.24 | 1.20 | 1.17 | 1.16 | 1.14 | 1.13 | 1.11 | 1.09 | 1.08 |
| f9 | 1.24 | 1.19 | 1.16 | 1.14 | 1.12 | 1.11 | 1.10 | 1.09 | 1.08 | 1.07 |
| f10 | 1.17 | 1.14 | 1.12 | 1.10 | 1.09 | 1.09 | 1.08 | 1.07 | 1.06 | 1.05 |
| f11 | 1.11 | 1.09 | 1.08 | 1.07 | 1.07 | 1.06 | 1.06 | 1.05 | 1.04 | 1.04 |
| f12 | 1.04 | 1.05 | 1.04 | 1.04 | 1.04 | 1.04 | 1.03 | 1.03 | 1.03 | 1.02 |
| SSiz | 100 | 200 | 300 | 400 | 500 | 600 | 800 | 1000 | 1500 | 2000 |
| Number of variables = 30 |
| f1 | 2.37 | 1.91 | 1.73 | 1.62 | 1.55 | 1.49 | 1.42 | 1.38 | 1.30 | 1.26 |
| f2 | 2.14 | 1.77 | 1.61 | 1.52 | 1.47 | 1.42 | 1.36 | 1.32 | 1.26 | 1.22 |
| f3 | 1.98 | 1.67 | 1.54 | 1.46 | 1.41 | 1.37 | 1.32 | 1.28 | 1.23 | 1.20 |
| f4 | 1.85 | 1.59 | 1.47 | 1.41 | 1.36 | 1.33 | 1.28 | 1.25 | 1.20 | 1.18 |
| f5 | 1.73 | 1.51 | 1.42 | 1.36 | 1.32 | 1.29 | 1.25 | 1.22 | 1.18 | 1.16 |
| f6 | 1.64 | 1.45 | 1.37 | 1.32 | 1.28 | 1.26 | 1.22 | 1.20 | 1.16 | 1.14 |
| f7 | 1.54 | 1.39 | 1.32 | 1.28 | 1.25 | 1.23 | 1.20 | 1.17 | 1.14 | 1.12 |
| f8 | 1.46 | 1.33 | 1.28 | 1.24 | 1.21 | 1.20 | 1.17 | 1.15 | 1.12 | 1.11 |
| f9 | 1.38 | 1.28 | 1.23 | 1.20 | 1.18 | 1.17 | 1.14 | 1.13 | 1.11 | 1.09 |
| f10 | 1.31 | 1.23 | 1.19 | 1.17 | 1.15 | 1.14 | 1.12 | 1.11 | 1.09 | 1.08 |
| f11 | 1.24 | 1.18 | 1.15 | 1.14 | 1.12 | 1.11 | 1.10 | 1.09 | 1.07 | 1.07 |
| f12 | 1.17 | 1.14 | 1.12 | 1.11 | 1.10 | 1.09 | 1.08 | 1.07 | 1.06 | 1.05 |
| f13 | 1.11 | 1.10 | 1.08 | 1.08 | 1.07 | 1.06 | 1.06 | 1.05 | 1.04 | 1.04 |
| f14 | 1.05 | 1.05 | 1.05 | 1.05 | 1.04 | 1.04 | 1.04 | 1.03 | 1.03 | 1.03 |
| f15 | | 1.01 | 1.01 | 1.02 | 1.02 | 1.02 | 1.02 | 1.02 | 1.01 | 1.01 |
| SSiz | 100 | 200 | 300 | 400 | 500 | 600 | 800 | 1000 | 1500 | 2000 |
| Number of variables = 35 |
| f1 | 2.51 | 2.00 | 1.79 | 1.67 | 1.60 | 1.54 | 1.46 | 1.41 | 1.33 | 1.28 |
| f2 | 2.27 | 1.85 | 1.68 | 1.58 | 1.52 | 1.46 | 1.40 | 1.35 | 1.29 | 1.25 |
| f3 | 2.12 | 1.76 | 1.60 | 1.52 | 1.46 | 1.41 | 1.36 | 1.32 | 1.26 | 1.22 |
| f4 | 1.98 | 1.67 | 1.54 | 1.46 | 1.41 | 1.38 | 1.32 | 1.29 | 1.23 | 1.20 |
| f5 | 1.87 | 1.60 | 1.48 | 1.42 | 1.37 | 1.34 | 1.29 | 1.26 | 1.21 | 1.18 |
| f6 | 1.77 | 1.53 | 1.43 | 1.37 | 1.33 | 1.30 | 1.26 | 1.23 | 1.19 | 1.16 |
| f7 | 1.67 | 1.47 | 1.39 | 1.33 | 1.30 | 1.27 | 1.23 | 1.21 | 1.17 | 1.15 |
| f8 | 1.59 | 1.42 | 1.34 | 1.30 | 1.26 | 1.24 | 1.21 | 1.19 | 1.15 | 1.13 |
| f9 | 1.51 | 1.37 | 1.30 | 1.26 | 1.23 | 1.21 | 1.19 | 1.17 | 1.14 | 1.12 |
| f10 | 1.43 | 1.32 | 1.26 | 1.23 | 1.20 | 1.19 | 1.16 | 1.15 | 1.12 | 1.10 |
| f11 | 1.36 | 1.27 | 1.22 | 1.20 | 1.18 | 1.16 | 1.14 | 1.13 | 1.10 | 1.09 |
| f12 | 1.29 | 1.22 | 1.19 | 1.17 | 1.15 | 1.14 | 1.12 | 1.11 | 1.09 | 1.08 |
| f13 | 1.23 | 1.18 | 1.15 | 1.14 | 1.12 | 1.11 | 1.10 | 1.09 | 1.08 | 1.07 |
| f14 | 1.16 | 1.14 | 1.12 | 1.11 | 1.10 | 1.09 | 1.08 | 1.07 | 1.06 | 1.05 |
| f15 | 1.10 | 1.10 | 1.08 | 1.08 | 1.07 | 1.07 | 1.06 | 1.05 | 1.05 | 1.04 |
| f16 | 1.04 | 1.06 | 1.05 | 1.05 | 1.05 | 1.05 | 1.04 | 1.04 | 1.03 | 1.03 |
| f17 | | 1.02 | 1.02 | 1.02 | 1.02 | 1.02 | 1.02 | 1.02 | 1.02 | 1.02 |
| SSiz | 100 | 200 | 300 | 400 | 500 | 600 | 800 | 1000 | 1500 | 2000 |
| Number of variables = 40 |
| f1 | 2.65 | 2.09 | 1.86 | 1.73 | 1.64 | 1.58 | 1.50 | 1.44 | 1.35 | 1.30 |
| f2 | 2.41 | 1.94 | 1.75 | 1.64 | 1.56 | 1.51 | 1.44 | 1.39 | 1.31 | 1.27 |
| f3 | 2.24 | 1.84 | 1.67 | 1.57 | 1.51 | 1.46 | 1.39 | 1.35 | 1.28 | 1.24 |
| f4 | 2.11 | 1.75 | 1.60 | 1.52 | 1.46 | 1.42 | 1.36 | 1.32 | 1.26 | 1.22 |
| f5 | 1.99 | 1.68 | 1.55 | 1.47 | 1.42 | 1.38 | 1.33 | 1.29 | 1.24 | 1.20 |
| f6 | 1.89 | 1.62 | 1.50 | 1.43 | 1.38 | 1.35 | 1.30 | 1.27 | 1.22 | 1.19 |
| f7 | 1.80 | 1.56 | 1.45 | 1.39 | 1.35 | 1.32 | 1.27 | 1.24 | 1.20 | 1.17 |
| f8 | 1.71 | 1.50 | 1.41 | 1.35 | 1.32 | 1.29 | 1.25 | 1.22 | 1.18 | 1.16 |
| f9 | 1.62 | 1.45 | 1.36 | 1.32 | 1.28 | 1.26 | 1.23 | 1.20 | 1.16 | 1.14 |
| f10 | 1.54 | 1.40 | 1.32 | 1.28 | 1.25 | 1.23 | 1.20 | 1.18 | 1.15 | 1.13 |
| f11 | 1.47 | 1.35 | 1.29 | 1.25 | 1.23 | 1.21 | 1.18 | 1.16 | 1.13 | 1.12 |
| f12 | 1.40 | 1.30 | 1.25 | 1.22 | 1.20 | 1.18 | 1.16 | 1.14 | 1.12 | 1.10 |
| f13 | 1.33 | 1.26 | 1.22 | 1.19 | 1.17 | 1.16 | 1.14 | 1.13 | 1.10 | 1.09 |
| f14 | 1.27 | 1.21 | 1.18 | 1.16 | 1.15 | 1.14 | 1.12 | 1.11 | 1.09 | 1.08 |
| f15 | 1.21 | 1.17 | 1.15 | 1.13 | 1.12 | 1.11 | 1.10 | 1.09 | 1.08 | 1.07 |
| f16 | 1.16 | 1.13 | 1.12 | 1.11 | 1.10 | 1.09 | 1.08 | 1.07 | 1.06 | 1.05 |
| f17 | 1.10 | 1.10 | 1.09 | 1.08 | 1.08 | 1.07 | 1.06 | 1.06 | 1.05 | 1.04 |
| f18 | 1.05 | 1.06 | 1.06 | 1.05 | 1.05 | 1.05 | 1.05 | 1.04 | 1.04 | 1.03 |
| f19 | | 1.02 | 1.03 | 1.03 | 1.03 | 1.03 | 1.03 | 1.03 | 1.02 | 1.02 |
| f20 | | | 1.00 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 |
| SSiz | 100 | 200 | 300 | 400 | 500 | 600 | 800 | 1000 | 1500 | 2000 |
| Number of variables = 45 |
| f1 | 2.78 | 2.17 | 1.92 | 1.78 | 1.69 | 1.62 | 1.53 | 1.47 | 1.38 | 1.32 |
| f2 | 2.53 | 2.02 | 1.81 | 1.69 | 1.61 | 1.55 | 1.47 | 1.42 | 1.34 | 1.29 |
| f3 | 2.36 | 1.91 | 1.73 | 1.62 | 1.55 | 1.50 | 1.43 | 1.38 | 1.31 | 1.26 |
| f4 | 2.23 | 1.83 | 1.67 | 1.57 | 1.51 | 1.46 | 1.39 | 1.35 | 1.28 | 1.24 |
| f5 | 2.11 | 1.76 | 1.61 | 1.52 | 1.46 | 1.42 | 1.36 | 1.32 | 1.26 | 1.23 |
| f6 | 2.01 | 1.69 | 1.56 | 1.48 | 1.43 | 1.39 | 1.34 | 1.30 | 1.24 | 1.21 |
| f7 | 1.91 | 1.63 | 1.51 | 1.44 | 1.39 | 1.36 | 1.31 | 1.27 | 1.22 | 1.19 |
| f8 | 1.82 | 1.57 | 1.47 | 1.40 | 1.36 | 1.33 | 1.28 | 1.25 | 1.21 | 1.18 |
| f9 | 1.73 | 1.52 | 1.42 | 1.37 | 1.33 | 1.30 | 1.26 | 1.23 | 1.19 | 1.16 |
| f10 | 1.66 | 1.47 | 1.38 | 1.33 | 1.30 | 1.27 | 1.24 | 1.21 | 1.17 | 1.15 |
| f11 | 1.58 | 1.42 | 1.35 | 1.30 | 1.27 | 1.25 | 1.22 | 1.19 | 1.16 | 1.14 |
| f12 | 1.52 | 1.38 | 1.31 | 1.27 | 1.25 | 1.22 | 1.20 | 1.17 | 1.14 | 1.13 |
| f13 | 1.45 | 1.33 | 1.28 | 1.25 | 1.22 | 1.20 | 1.18 | 1.16 | 1.13 | 1.11 |
| f14 | 1.38 | 1.29 | 1.24 | 1.22 | 1.20 | 1.18 | 1.16 | 1.14 | 1.12 | 1.10 |
| f15 | 1.32 | 1.25 | 1.21 | 1.19 | 1.17 | 1.16 | 1.14 | 1.12 | 1.10 | 1.09 |
| f16 | 1.26 | 1.21 | 1.18 | 1.16 | 1.14 | 1.13 | 1.12 | 1.11 | 1.09 | 1.08 |
| f17 | 1.20 | 1.17 | 1.15 | 1.13 | 1.12 | 1.11 | 1.10 | 1.09 | 1.08 | 1.07 |
| f18 | 1.15 | 1.13 | 1.12 | 1.11 | 1.10 | 1.09 | 1.08 | 1.07 | 1.06 | 1.06 |
| f19 | 1.09 | 1.10 | 1.09 | 1.08 | 1.08 | 1.07 | 1.07 | 1.06 | 1.05 | 1.04 |
| f20 | 1.05 | 1.06 | 1.06 | 1.06 | 1.05 | 1.05 | 1.05 | 1.04 | 1.04 | 1.03 |
| f21 | | 1.03 | 1.03 | 1.03 | 1.03 | 1.03 | 1.03 | 1.03 | 1.03 | 1.02 |
| f22 | | | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 |
| SSiz | 100 | 200 | 300 | 400 | 500 | 600 | 800 | 1000 | 1500 | 2000 |
| Number of variables = 50 |
| f1 | 2.91 | 2.24 | 1.99 | 1.83 | 1.73 | 1.66 | 1.56 | 1.50 | 1.40 | 1.34 |
| f2 | 2.65 | 2.10 | 1.87 | 1.74 | 1.65 | 1.59 | 1.50 | 1.45 | 1.36 | 1.31 |
| f3 | 2.49 | 1.99 | 1.79 | 1.67 | 1.60 | 1.54 | 1.46 | 1.41 | 1.33 | 1.28 |
| f4 | 2.35 | 1.91 | 1.72 | 1.62 | 1.55 | 1.50 | 1.43 | 1.38 | 1.31 | 1.26 |
| f5 | 2.22 | 1.84 | 1.67 | 1.57 | 1.51 | 1.46 | 1.39 | 1.35 | 1.28 | 1.25 |
| f6 | 2.12 | 1.77 | 1.62 | 1.53 | 1.47 | 1.43 | 1.37 | 1.33 | 1.26 | 1.23 |
| f7 | 2.02 | 1.71 | 1.57 | 1.49 | 1.44 | 1.40 | 1.34 | 1.30 | 1.25 | 1.21 |
| f8 | 1.93 | 1.65 | 1.53 | 1.45 | 1.40 | 1.37 | 1.32 | 1.28 | 1.23 | 1.20 |
| f9 | 1.84 | 1.59 | 1.48 | 1.42 | 1.37 | 1.34 | 1.29 | 1.26 | 1.21 | 1.18 |
| f10 | 1.76 | 1.54 | 1.44 | 1.38 | 1.34 | 1.31 | 1.27 | 1.24 | 1.20 | 1.17 |
| f11 | 1.69 | 1.49 | 1.41 | 1.35 | 1.32 | 1.29 | 1.25 | 1.22 | 1.18 | 1.16 |
| f12 | 1.62 | 1.45 | 1.37 | 1.32 | 1.29 | 1.26 | 1.23 | 1.21 | 1.17 | 1.15 |
| f13 | 1.55 | 1.40 | 1.33 | 1.29 | 1.26 | 1.24 | 1.21 | 1.19 | 1.15 | 1.13 |
| f14 | 1.48 | 1.36 | 1.30 | 1.26 | 1.24 | 1.22 | 1.19 | 1.17 | 1.14 | 1.12 |
| f15 | 1.42 | 1.32 | 1.27 | 1.24 | 1.21 | 1.20 | 1.17 | 1.15 | 1.13 | 1.11 |
| f16 | 1.36 | 1.28 | 1.24 | 1.21 | 1.19 | 1.18 | 1.15 | 1.14 | 1.11 | 1.10 |
| f17 | 1.30 | 1.24 | 1.20 | 1.18 | 1.17 | 1.16 | 1.13 | 1.12 | 1.10 | 1.09 |
| f18 | 1.24 | 1.20 | 1.18 | 1.16 | 1.14 | 1.13 | 1.12 | 1.11 | 1.09 | 1.08 |
| f19 | 1.19 | 1.17 | 1.15 | 1.13 | 1.12 | 1.11 | 1.10 | 1.09 | 1.08 | 1.07 |
| f20 | 1.14 | 1.13 | 1.12 | 1.11 | 1.10 | 1.09 | 1.08 | 1.08 | 1.06 | 1.06 |
| f21 | 1.09 | 1.09 | 1.09 | 1.09 | 1.08 | 1.07 | 1.07 | 1.06 | 1.05 | 1.05 |
| f22 | 1.04 | 1.06 | 1.06 | 1.06 | 1.06 | 1.06 | 1.05 | 1.05 | 1.04 | 1.04 |
| f23 | | 1.03 | 1.04 | 1.04 | 1.04 | 1.04 | 1.03 | 1.03 | 1.03 | 1.03 |
| f24 | | | 1.01 | 1.02 | 1.02 | 1.02 | 1.02 | 1.02 | 1.02 | 1.02 |
| f25 | | | | | | | | | 1.01 | 1.01 |
| SSiz | 250 | 500 | 750 | 1000 | 1250 | 1500 | 1750 | 2000 | 3000 | 4000 |
| Number of variables = 60 |
| f1 | 2.22 | 1.81 | 1.65 | 1.55 | 1.49 | 1.44 | 1.40 | 1.38 | 1.30 | 1.26 |
| f2 | 2.09 | 1.73 | 1.59 | 1.50 | 1.44 | 1.40 | 1.37 | 1.34 | 1.28 | 1.24 |
| f3 | 2.00 | 1.68 | 1.54 | 1.46 | 1.41 | 1.37 | 1.34 | 1.32 | 1.26 | 1.22 |
| f4 | 1.93 | 1.63 | 1.51 | 1.43 | 1.38 | 1.35 | 1.32 | 1.30 | 1.24 | 1.21 |
| f5 | 1.86 | 1.59 | 1.47 | 1.40 | 1.36 | 1.33 | 1.30 | 1.28 | 1.23 | 1.20 |
| f6 | 1.80 | 1.55 | 1.44 | 1.38 | 1.34 | 1.31 | 1.29 | 1.27 | 1.22 | 1.19 |
| f7 | 1.75 | 1.52 | 1.42 | 1.36 | 1.32 | 1.29 | 1.27 | 1.25 | 1.20 | 1.18 |
| f8 | 1.70 | 1.49 | 1.39 | 1.34 | 1.30 | 1.27 | 1.25 | 1.24 | 1.19 | 1.17 |
| f9 | 1.65 | 1.46 | 1.37 | 1.32 | 1.28 | 1.26 | 1.24 | 1.22 | 1.18 | 1.16 |
| f10 | 1.61 | 1.43 | 1.35 | 1.30 | 1.27 | 1.24 | 1.22 | 1.21 | 1.17 | 1.15 |
| f11 | 1.57 | 1.40 | 1.32 | 1.28 | 1.25 | 1.23 | 1.21 | 1.20 | 1.16 | 1.14 |
| f12 | 1.52 | 1.37 | 1.30 | 1.26 | 1.23 | 1.21 | 1.20 | 1.19 | 1.15 | 1.13 |
| f13 | 1.48 | 1.34 | 1.28 | 1.25 | 1.22 | 1.20 | 1.19 | 1.17 | 1.14 | 1.12 |
| f14 | 1.45 | 1.32 | 1.26 | 1.23 | 1.20 | 1.19 | 1.17 | 1.16 | 1.13 | 1.11 |
| f15 | 1.41 | 1.30 | 1.24 | 1.21 | 1.19 | 1.17 | 1.16 | 1.15 | 1.12 | 1.11 |
| f16 | 1.37 | 1.27 | 1.22 | 1.20 | 1.18 | 1.16 | 1.15 | 1.14 | 1.11 | 1.10 |
| f17 | 1.34 | 1.25 | 1.21 | 1.18 | 1.16 | 1.15 | 1.14 | 1.13 | 1.11 | 1.09 |
| f18 | 1.31 | 1.23 | 1.19 | 1.17 | 1.15 | 1.14 | 1.13 | 1.12 | 1.10 | 1.09 |
| f19 | 1.27 | 1.20 | 1.17 | 1.15 | 1.13 | 1.12 | 1.12 | 1.11 | 1.09 | 1.08 |
| f20 | 1.24 | 1.18 | 1.15 | 1.14 | 1.12 | 1.11 | 1.10 | 1.10 | 1.08 | 1.07 |
| f21 | 1.21 | 1.16 | 1.14 | 1.12 | 1.11 | 1.10 | 1.09 | 1.09 | 1.07 | 1.06 |
| f22 | 1.18 | 1.14 | 1.12 | 1.11 | 1.10 | 1.09 | 1.08 | 1.08 | 1.07 | 1.06 |
| f23 | 1.15 | 1.12 | 1.10 | 1.09 | 1.08 | 1.08 | 1.07 | 1.07 | 1.06 | 1.05 |
| f24 | 1.12 | 1.10 | 1.09 | 1.08 | 1.07 | 1.07 | 1.06 | 1.06 | 1.05 | 1.04 |
| f25 | 1.09 | 1.08 | 1.07 | 1.06 | 1.06 | 1.06 | 1.05 | 1.05 | 1.04 | 1.04 |
| f26 | 1.07 | 1.06 | 1.06 | 1.05 | 1.05 | 1.05 | 1.04 | 1.04 | 1.03 | 1.03 |
| f27 | 1.04 | 1.04 | 1.04 | 1.04 | 1.04 | 1.03 | 1.03 | 1.03 | 1.03 | 1.02 |
| f28 | 1.01 | 1.02 | 1.03 | 1.03 | 1.02 | 1.02 | 1.02 | 1.02 | 1.02 | 1.02 |
| f29 | | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 |
| SSiz | 250 | 500 | 750 | 1000 | 1250 | 1500 | 1750 | 2000 | 3000 | 4000 |
| SSiz | 250 | 500 | 750 | 1000 | 1250 | 1500 | 1750 | 2000 | 3000 | 4000 |
| Number of variables = 70 |
| f1 | 2.35 | 1.89 | 1.71 | 1.60 | 1.53 | 1.48 | 1.44 | 1.41 | 1.33 | 1.28 |
| f2 | 2.21 | 1.81 | 1.64 | 1.55 | 1.49 | 1.44 | 1.40 | 1.38 | 1.30 | 1.26 |
| f3 | 2.12 | 1.75 | 1.60 | 1.51 | 1.46 | 1.41 | 1.38 | 1.35 | 1.28 | 1.24 |
| f4 | 2.04 | 1.71 | 1.56 | 1.48 | 1.43 | 1.39 | 1.36 | 1.33 | 1.27 | 1.23 |
| f5 | 1.98 | 1.67 | 1.53 | 1.46 | 1.41 | 1.37 | 1.34 | 1.32 | 1.26 | 1.22 |
| f6 | 1.92 | 1.63 | 1.50 | 1.43 | 1.38 | 1.35 | 1.32 | 1.30 | 1.24 | 1.21 |
| f7 | 1.86 | 1.59 | 1.48 | 1.41 | 1.36 | 1.33 | 1.31 | 1.29 | 1.23 | 1.20 |
| f8 | 1.81 | 1.56 | 1.45 | 1.39 | 1.35 | 1.32 | 1.29 | 1.27 | 1.22 | 1.19 |
| f9 | 1.76 | 1.53 | 1.43 | 1.37 | 1.33 | 1.30 | 1.28 | 1.26 | 1.21 | 1.18 |
| f10 | 1.72 | 1.50 | 1.41 | 1.35 | 1.31 | 1.28 | 1.26 | 1.24 | 1.20 | 1.17 |
| f11 | 1.67 | 1.47 | 1.38 | 1.33 | 1.30 | 1.27 | 1.25 | 1.23 | 1.19 | 1.16 |
| f12 | 1.63 | 1.45 | 1.36 | 1.31 | 1.28 | 1.26 | 1.24 | 1.22 | 1.18 | 1.16 |
| f13 | 1.60 | 1.42 | 1.34 | 1.30 | 1.26 | 1.24 | 1.22 | 1.21 | 1.17 | 1.15 |
| f14 | 1.56 | 1.40 | 1.32 | 1.28 | 1.25 | 1.23 | 1.21 | 1.20 | 1.16 | 1.14 |
| f15 | 1.52 | 1.37 | 1.30 | 1.26 | 1.24 | 1.22 | 1.20 | 1.19 | 1.15 | 1.13 |
| f16 | 1.48 | 1.35 | 1.29 | 1.25 | 1.22 | 1.20 | 1.19 | 1.18 | 1.14 | 1.13 |
| f17 | 1.45 | 1.32 | 1.27 | 1.23 | 1.21 | 1.19 | 1.18 | 1.17 | 1.14 | 1.12 |
| f18 | 1.42 | 1.30 | 1.25 | 1.22 | 1.19 | 1.18 | 1.17 | 1.16 | 1.13 | 1.11 |
| f19 | 1.38 | 1.28 | 1.23 | 1.20 | 1.18 | 1.17 | 1.15 | 1.15 | 1.12 | 1.10 |
| f20 | 1.35 | 1.26 | 1.22 | 1.19 | 1.17 | 1.16 | 1.14 | 1.14 | 1.11 | 1.10 |
| f21 | 1.32 | 1.24 | 1.20 | 1.17 | 1.16 | 1.14 | 1.13 | 1.13 | 1.10 | 1.09 |
| f22 | 1.29 | 1.22 | 1.18 | 1.16 | 1.14 | 1.13 | 1.12 | 1.12 | 1.10 | 1.08 |
| f23 | 1.26 | 1.20 | 1.17 | 1.15 | 1.13 | 1.12 | 1.11 | 1.11 | 1.09 | 1.08 |
| f24 | 1.23 | 1.18 | 1.15 | 1.13 | 1.12 | 1.11 | 1.10 | 1.10 | 1.08 | 1.07 |
| f25 | 1.20 | 1.16 | 1.13 | 1.12 | 1.11 | 1.10 | 1.09 | 1.09 | 1.07 | 1.06 |
| f26 | 1.17 | 1.14 | 1.12 | 1.11 | 1.10 | 1.09 | 1.08 | 1.08 | 1.07 | 1.06 |
| f27 | 1.15 | 1.12 | 1.10 | 1.09 | 1.09 | 1.08 | 1.07 | 1.07 | 1.06 | 1.05 |
| f28 | 1.12 | 1.10 | 1.09 | 1.08 | 1.07 | 1.07 | 1.07 | 1.06 | 1.05 | 1.05 |
| f29 | 1.09 | 1.08 | 1.08 | 1.07 | 1.06 | 1.06 | 1.06 | 1.05 | 1.04 | 1.04 |
| f30 | 1.07 | 1.07 | 1.06 | 1.06 | 1.05 | 1.05 | 1.05 | 1.04 | 1.04 | 1.03 |
| f31 | 1.04 | 1.05 | 1.05 | 1.04 | 1.04 | 1.04 | 1.04 | 1.04 | 1.03 | 1.03 |
| f32 | 1.02 | 1.03 | 1.03 | 1.03 | 1.03 | 1.03 | 1.03 | 1.03 | 1.02 | 1.02 |
| f33 | | 1.01 | 1.02 | 1.02 | 1.02 | 1.02 | 1.02 | 1.02 | 1.02 | 1.02 |
| f34 | | | | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 |
| SSiz | 250 | 500 | 750 | 1000 | 1250 | 1500 | 1750 | 2000 | 3000 | 4000 |
| SSiz | 250 | 500 | 750 | 1000 | 1250 | 1500 | 1750 | 2000 | 3000 | 4000 |
| Number of variables = 80 |
| f1 | 2.45 | 1.96 | 1.76 | 1.65 | 1.57 | 1.52 | 1.48 | 1.44 | 1.35 | 1.30 |
| f2 | 2.32 | 1.88 | 1.70 | 1.60 | 1.53 | 1.48 | 1.44 | 1.41 | 1.33 | 1.28 |
| f3 | 2.23 | 1.82 | 1.66 | 1.56 | 1.50 | 1.45 | 1.41 | 1.39 | 1.31 | 1.27 |
| f4 | 2.15 | 1.78 | 1.62 | 1.53 | 1.47 | 1.43 | 1.39 | 1.37 | 1.29 | 1.25 |
| f5 | 2.09 | 1.74 | 1.59 | 1.50 | 1.45 | 1.40 | 1.37 | 1.35 | 1.28 | 1.24 |
| f6 | 2.03 | 1.70 | 1.56 | 1.48 | 1.43 | 1.39 | 1.36 | 1.33 | 1.27 | 1.23 |
| f7 | 1.97 | 1.66 | 1.53 | 1.46 | 1.41 | 1.37 | 1.34 | 1.32 | 1.26 | 1.22 |
| f8 | 1.92 | 1.63 | 1.51 | 1.44 | 1.39 | 1.35 | 1.33 | 1.30 | 1.25 | 1.21 |
| f9 | 1.87 | 1.60 | 1.49 | 1.42 | 1.37 | 1.34 | 1.31 | 1.29 | 1.23 | 1.20 |
| f10 | 1.83 | 1.57 | 1.46 | 1.40 | 1.35 | 1.32 | 1.30 | 1.28 | 1.23 | 1.19 |
| f11 | 1.78 | 1.54 | 1.44 | 1.38 | 1.34 | 1.31 | 1.28 | 1.27 | 1.22 | 1.19 |
| f12 | 1.74 | 1.52 | 1.42 | 1.36 | 1.32 | 1.29 | 1.27 | 1.25 | 1.21 | 1.18 |
| f13 | 1.70 | 1.49 | 1.40 | 1.34 | 1.31 | 1.28 | 1.26 | 1.24 | 1.20 | 1.17 |
| f14 | 1.66 | 1.47 | 1.38 | 1.33 | 1.29 | 1.27 | 1.25 | 1.23 | 1.19 | 1.16 |
| f15 | 1.62 | 1.44 | 1.36 | 1.31 | 1.28 | 1.25 | 1.24 | 1.22 | 1.18 | 1.16 |
| f16 | 1.59 | 1.42 | 1.34 | 1.30 | 1.27 | 1.24 | 1.22 | 1.21 | 1.17 | 1.15 |
| f17 | 1.55 | 1.40 | 1.32 | 1.28 | 1.25 | 1.23 | 1.21 | 1.20 | 1.16 | 1.14 |
| f18 | 1.52 | 1.37 | 1.31 | 1.27 | 1.24 | 1.22 | 1.20 | 1.19 | 1.15 | 1.13 |
| f19 | 1.48 | 1.35 | 1.29 | 1.25 | 1.23 | 1.21 | 1.19 | 1.18 | 1.15 | 1.13 |
| f20 | 1.45 | 1.33 | 1.27 | 1.24 | 1.21 | 1.20 | 1.18 | 1.17 | 1.14 | 1.12 |
| f21 | 1.42 | 1.31 | 1.26 | 1.22 | 1.20 | 1.18 | 1.17 | 1.16 | 1.13 | 1.11 |
| f22 | 1.39 | 1.29 | 1.24 | 1.21 | 1.19 | 1.17 | 1.16 | 1.15 | 1.12 | 1.11 |
| f23 | 1.36 | 1.27 | 1.22 | 1.20 | 1.18 | 1.16 | 1.15 | 1.14 | 1.12 | 1.10 |
| f24 | 1.33 | 1.25 | 1.21 | 1.18 | 1.17 | 1.15 | 1.14 | 1.13 | 1.11 | 1.10 |
| f25 | 1.30 | 1.23 | 1.19 | 1.17 | 1.15 | 1.14 | 1.13 | 1.12 | 1.10 | 1.09 |
| f26 | 1.27 | 1.21 | 1.18 | 1.16 | 1.14 | 1.13 | 1.12 | 1.11 | 1.09 | 1.08 |
| f27 | 1.25 | 1.19 | 1.16 | 1.14 | 1.13 | 1.12 | 1.11 | 1.11 | 1.09 | 1.08 |
| f28 | 1.22 | 1.17 | 1.15 | 1.13 | 1.12 | 1.11 | 1.10 | 1.10 | 1.08 | 1.07 |
| f29 | 1.19 | 1.15 | 1.13 | 1.12 | 1.11 | 1.10 | 1.09 | 1.09 | 1.07 | 1.06 |
| f30 | 1.17 | 1.14 | 1.12 | 1.11 | 1.10 | 1.09 | 1.08 | 1.08 | 1.07 | 1.06 |
| f31 | 1.14 | 1.12 | 1.10 | 1.09 | 1.09 | 1.08 | 1.08 | 1.07 | 1.06 | 1.05 |
| f32 | 1.11 | 1.10 | 1.09 | 1.08 | 1.08 | 1.07 | 1.07 | 1.06 | 1.05 | 1.05 |
| f33 | 1.09 | 1.09 | 1.08 | 1.07 | 1.07 | 1.06 | 1.06 | 1.05 | 1.05 | 1.04 |
| f34 | 1.07 | 1.07 | 1.06 | 1.06 | 1.06 | 1.05 | 1.05 | 1.05 | 1.04 | 1.04 |
| f35 | 1.04 | 1.05 | 1.05 | 1.05 | 1.05 | 1.04 | 1.04 | 1.04 | 1.03 | 1.03 |
| f36 | 1.02 | 1.04 | 1.04 | 1.04 | 1.04 | 1.03 | 1.03 | 1.03 | 1.03 | 1.02 |
| f37 | | 1.02 | 1.02 | 1.02 | 1.03 | 1.02 | 1.02 | 1.02 | 1.02 | 1.02 |
| f38 | | | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 |
| f39 | | | | | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 |
| SSiz | 250 | 500 | 750 | 1000 | 1250 | 1500 | 1750 | 2000 | 3000 | 4000 |
| SSiz | 250 | 500 | 750 | 1000 | 1250 | 1500 | 1750 | 2000 | 3000 | 4000 |
| Number of variables = 90 |
| f1 | 2.56 | 2.03 | 1.82 | 1.69 | 1.61 | 1.55 | 1.51 | 1.47 | 1.38 | 1.32 |
| f2 | 2.43 | 1.95 | 1.76 | 1.64 | 1.57 | 1.51 | 1.47 | 1.44 | 1.35 | 1.30 |
| f3 | 2.34 | 1.89 | 1.71 | 1.61 | 1.54 | 1.48 | 1.44 | 1.41 | 1.33 | 1.29 |
| f4 | 2.26 | 1.84 | 1.67 | 1.58 | 1.51 | 1.46 | 1.42 | 1.39 | 1.32 | 1.27 |
| f5 | 2.19 | 1.80 | 1.64 | 1.55 | 1.49 | 1.44 | 1.41 | 1.38 | 1.31 | 1.26 |
| f6 | 2.13 | 1.77 | 1.61 | 1.52 | 1.47 | 1.42 | 1.39 | 1.36 | 1.29 | 1.25 |
| f7 | 2.08 | 1.73 | 1.59 | 1.50 | 1.45 | 1.40 | 1.37 | 1.35 | 1.28 | 1.24 |
| f8 | 2.03 | 1.70 | 1.56 | 1.48 | 1.43 | 1.39 | 1.36 | 1.33 | 1.27 | 1.23 |
| f9 | 1.98 | 1.67 | 1.54 | 1.46 | 1.41 | 1.37 | 1.34 | 1.32 | 1.26 | 1.22 |
| f10 | 1.93 | 1.64 | 1.51 | 1.44 | 1.39 | 1.36 | 1.33 | 1.31 | 1.25 | 1.22 |
| f11 | 1.89 | 1.61 | 1.49 | 1.42 | 1.38 | 1.34 | 1.32 | 1.30 | 1.24 | 1.21 |
| f12 | 1.84 | 1.59 | 1.47 | 1.41 | 1.36 | 1.33 | 1.30 | 1.28 | 1.23 | 1.20 |
| f13 | 1.80 | 1.56 | 1.45 | 1.39 | 1.35 | 1.32 | 1.29 | 1.27 | 1.22 | 1.19 |
| f14 | 1.76 | 1.53 | 1.43 | 1.37 | 1.33 | 1.30 | 1.28 | 1.26 | 1.21 | 1.18 |
| f15 | 1.72 | 1.51 | 1.41 | 1.36 | 1.32 | 1.29 | 1.27 | 1.25 | 1.20 | 1.18 |
| f16 | 1.69 | 1.49 | 1.40 | 1.34 | 1.31 | 1.28 | 1.26 | 1.24 | 1.20 | 1.17 |
| f17 | 1.65 | 1.46 | 1.38 | 1.33 | 1.29 | 1.27 | 1.25 | 1.23 | 1.19 | 1.16 |
| f18 | 1.62 | 1.44 | 1.36 | 1.31 | 1.28 | 1.25 | 1.24 | 1.22 | 1.18 | 1.16 |
| f19 | 1.58 | 1.42 | 1.34 | 1.30 | 1.27 | 1.24 | 1.23 | 1.21 | 1.17 | 1.15 |
| f20 | 1.55 | 1.40 | 1.33 | 1.28 | 1.25 | 1.23 | 1.21 | 1.20 | 1.16 | 1.14 |
| f21 | 1.52 | 1.37 | 1.31 | 1.27 | 1.24 | 1.22 | 1.20 | 1.19 | 1.16 | 1.14 |
| f22 | 1.49 | 1.35 | 1.29 | 1.26 | 1.23 | 1.21 | 1.19 | 1.18 | 1.15 | 1.13 |
| f23 | 1.46 | 1.33 | 1.28 | 1.24 | 1.22 | 1.20 | 1.19 | 1.17 | 1.14 | 1.12 |
| f24 | 1.43 | 1.32 | 1.26 | 1.23 | 1.21 | 1.19 | 1.18 | 1.17 | 1.14 | 1.12 |
| f25 | 1.40 | 1.30 | 1.25 | 1.22 | 1.19 | 1.18 | 1.17 | 1.16 | 1.13 | 1.11 |
| f26 | 1.37 | 1.28 | 1.23 | 1.20 | 1.18 | 1.17 | 1.16 | 1.15 | 1.12 | 1.11 |
| f27 | 1.34 | 1.26 | 1.22 | 1.19 | 1.17 | 1.16 | 1.15 | 1.14 | 1.11 | 1.10 |
| f28 | 1.31 | 1.24 | 1.20 | 1.18 | 1.16 | 1.15 | 1.14 | 1.13 | 1.11 | 1.09 |
| f29 | 1.29 | 1.22 | 1.19 | 1.17 | 1.15 | 1.14 | 1.13 | 1.12 | 1.10 | 1.09 |
| f30 | 1.26 | 1.20 | 1.17 | 1.15 | 1.14 | 1.13 | 1.12 | 1.11 | 1.09 | 1.08 |
| f31 | 1.23 | 1.19 | 1.16 | 1.14 | 1.13 | 1.12 | 1.11 | 1.11 | 1.09 | 1.08 |
| f32 | 1.21 | 1.17 | 1.14 | 1.13 | 1.12 | 1.11 | 1.10 | 1.10 | 1.08 | 1.07 |
| f33 | 1.18 | 1.15 | 1.13 | 1.12 | 1.11 | 1.10 | 1.09 | 1.09 | 1.07 | 1.07 |
| f34 | 1.16 | 1.14 | 1.12 | 1.11 | 1.10 | 1.09 | 1.08 | 1.08 | 1.07 | 1.06 |
| f35 | 1.13 | 1.12 | 1.11 | 1.09 | 1.09 | 1.08 | 1.08 | 1.07 | 1.06 | 1.05 |
| f36 | 1.11 | 1.10 | 1.09 | 1.08 | 1.08 | 1.07 | 1.07 | 1.06 | 1.06 | 1.05 |
| f37 | 1.09 | 1.09 | 1.08 | 1.07 | 1.07 | 1.06 | 1.06 | 1.06 | 1.05 | 1.04 |
| f38 | 1.06 | 1.07 | 1.07 | 1.06 | 1.06 | 1.06 | 1.05 | 1.05 | 1.04 | 1.04 |
| f39 | 1.04 | 1.05 | 1.05 | 1.05 | 1.05 | 1.05 | 1.04 | 1.04 | 1.04 | 1.03 |
| f40 | 1.02 | 1.04 | 1.04 | 1.04 | 1.04 | 1.04 | 1.04 | 1.03 | 1.03 | 1.03 |
| f41 | | 1.02 | 1.03 | 1.03 | 1.03 | 1.03 | 1.03 | 1.03 | 1.02 | 1.02 |
| f42 | | 1.01 | 1.02 | 1.02 | 1.02 | 1.02 | 1.02 | 1.02 | 1.02 | 1.02 |
| f43 | | | | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 |
| f44 | | | | | | | | | 1.01 | 1.01 |
| SSiz | 250 | 500 | 750 | 1000 | 1250 | 1500 | 1750 | 2000 | 3000 | 4000 |
| SSiz | 250 | 500 | 750 | 1000 | 1250 | 1500 | 1750 | 2000 | 3000 | 4000 |
| Number of variables = 100 |
| f1 | 2.67 | 2.10 | 1.87 | 1.74 | 1.65 | 1.59 | 1.54 | 1.50 | 1.40 | 1.34 |
| f2 | 2.53 | 2.02 | 1.81 | 1.68 | 1.61 | 1.55 | 1.50 | 1.47 | 1.37 | 1.32 |
| f3 | 2.44 | 1.96 | 1.76 | 1.65 | 1.57 | 1.52 | 1.48 | 1.44 | 1.36 | 1.31 |
| f4 | 2.36 | 1.91 | 1.73 | 1.62 | 1.55 | 1.50 | 1.46 | 1.42 | 1.34 | 1.29 |
| f5 | 2.29 | 1.87 | 1.69 | 1.59 | 1.52 | 1.47 | 1.44 | 1.41 | 1.33 | 1.28 |
| f6 | 2.23 | 1.83 | 1.66 | 1.57 | 1.50 | 1.46 | 1.42 | 1.39 | 1.32 | 1.27 |
| f7 | 2.18 | 1.80 | 1.64 | 1.55 | 1.48 | 1.44 | 1.40 | 1.38 | 1.30 | 1.26 |
| f8 | 2.13 | 1.76 | 1.61 | 1.52 | 1.47 | 1.42 | 1.39 | 1.36 | 1.29 | 1.25 |
| f9 | 2.08 | 1.73 | 1.59 | 1.50 | 1.45 | 1.41 | 1.38 | 1.35 | 1.28 | 1.24 |
| f10 | 2.03 | 1.70 | 1.57 | 1.49 | 1.43 | 1.39 | 1.36 | 1.34 | 1.27 | 1.24 |
| f11 | 1.98 | 1.68 | 1.54 | 1.47 | 1.42 | 1.38 | 1.35 | 1.33 | 1.26 | 1.23 |
| f12 | 1.94 | 1.65 | 1.52 | 1.45 | 1.40 | 1.36 | 1.34 | 1.31 | 1.25 | 1.22 |
| f13 | 1.90 | 1.62 | 1.50 | 1.43 | 1.39 | 1.35 | 1.32 | 1.30 | 1.25 | 1.21 |
| f14 | 1.86 | 1.60 | 1.48 | 1.42 | 1.37 | 1.34 | 1.31 | 1.29 | 1.24 | 1.20 |
| f15 | 1.82 | 1.57 | 1.47 | 1.40 | 1.36 | 1.33 | 1.30 | 1.28 | 1.23 | 1.20 |
| f16 | 1.78 | 1.55 | 1.45 | 1.39 | 1.34 | 1.31 | 1.29 | 1.27 | 1.22 | 1.19 |
| f17 | 1.75 | 1.53 | 1.43 | 1.37 | 1.33 | 1.30 | 1.28 | 1.26 | 1.21 | 1.18 |
| f18 | 1.71 | 1.50 | 1.41 | 1.36 | 1.32 | 1.29 | 1.27 | 1.25 | 1.20 | 1.18 |
| f19 | 1.68 | 1.48 | 1.39 | 1.34 | 1.30 | 1.28 | 1.26 | 1.24 | 1.20 | 1.17 |
| f20 | 1.65 | 1.46 | 1.38 | 1.33 | 1.29 | 1.27 | 1.25 | 1.23 | 1.19 | 1.16 |
| f21 | 1.61 | 1.44 | 1.36 | 1.31 | 1.28 | 1.26 | 1.24 | 1.22 | 1.18 | 1.16 |
| f22 | 1.58 | 1.42 | 1.34 | 1.30 | 1.27 | 1.25 | 1.23 | 1.21 | 1.17 | 1.15 |
| f23 | 1.55 | 1.40 | 1.33 | 1.29 | 1.26 | 1.23 | 1.22 | 1.20 | 1.17 | 1.15 |
| f24 | 1.52 | 1.38 | 1.31 | 1.27 | 1.24 | 1.22 | 1.21 | 1.19 | 1.16 | 1.14 |
| f25 | 1.49 | 1.36 | 1.30 | 1.26 | 1.23 | 1.21 | 1.20 | 1.19 | 1.15 | 1.13 |
| f26 | 1.46 | 1.34 | 1.28 | 1.25 | 1.22 | 1.20 | 1.19 | 1.18 | 1.15 | 1.13 |
| f27 | 1.43 | 1.32 | 1.27 | 1.23 | 1.21 | 1.19 | 1.18 | 1.17 | 1.14 | 1.12 |
| f28 | 1.40 | 1.30 | 1.25 | 1.22 | 1.20 | 1.18 | 1.17 | 1.16 | 1.13 | 1.12 |
| f29 | 1.38 | 1.29 | 1.24 | 1.21 | 1.19 | 1.17 | 1.16 | 1.15 | 1.13 | 1.11 |
| f30 | 1.35 | 1.27 | 1.22 | 1.20 | 1.18 | 1.16 | 1.15 | 1.14 | 1.12 | 1.10 |
| f31 | 1.32 | 1.25 | 1.21 | 1.19 | 1.17 | 1.16 | 1.15 | 1.14 | 1.11 | 1.10 |
| f32 | 1.30 | 1.23 | 1.20 | 1.17 | 1.16 | 1.15 | 1.14 | 1.13 | 1.11 | 1.09 |
| f33 | 1.27 | 1.22 | 1.18 | 1.16 | 1.15 | 1.14 | 1.13 | 1.12 | 1.10 | 1.09 |
| f34 | 1.25 | 1.20 | 1.17 | 1.15 | 1.14 | 1.13 | 1.12 | 1.11 | 1.09 | 1.08 |
| f35 | 1.22 | 1.18 | 1.16 | 1.14 | 1.13 | 1.12 | 1.11 | 1.10 | 1.09 | 1.08 |
| f36 | 1.20 | 1.17 | 1.14 | 1.13 | 1.12 | 1.11 | 1.10 | 1.10 | 1.08 | 1.07 |
| f37 | 1.17 | 1.15 | 1.13 | 1.12 | 1.11 | 1.10 | 1.09 | 1.09 | 1.07 | 1.07 |
| f38 | 1.15 | 1.13 | 1.12 | 1.11 | 1.10 | 1.09 | 1.09 | 1.08 | 1.07 | 1.06 |
| f39 | 1.13 | 1.12 | 1.11 | 1.10 | 1.09 | 1.08 | 1.08 | 1.07 | 1.06 | 1.06 |
| f40 | 1.11 | 1.10 | 1.09 | 1.09 | 1.08 | 1.07 | 1.07 | 1.07 | 1.06 | 1.05 |
| f41 | 1.08 | 1.09 | 1.08 | 1.07 | 1.07 | 1.07 | 1.06 | 1.06 | 1.05 | 1.05 |
| f42 | 1.06 | 1.07 | 1.07 | 1.06 | 1.06 | 1.06 | 1.05 | 1.05 | 1.04 | 1.04 |
| f43 | 1.04 | 1.06 | 1.06 | 1.05 | 1.05 | 1.05 | 1.05 | 1.04 | 1.04 | 1.03 |
| f44 | 1.02 | 1.04 | 1.04 | 1.04 | 1.04 | 1.04 | 1.04 | 1.04 | 1.03 | 1.03 |
| f45 | | 1.03 | 1.03 | 1.03 | 1.03 | 1.03 | 1.03 | 1.03 | 1.03 | 1.02 |
| f46 | | 1.01 | 1.02 | 1.02 | 1.02 | 1.02 | 1.02 | 1.02 | 1.02 | 1.02 |
| f47 | | | 1.01 | 1.01 | 1.02 | 1.02 | 1.02 | 1.02 | 1.02 | 1.01 |
| f48 | | | | | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 |
| SSiz | 250 | 500 | 750 | 1000 | 1250 | 1500 | 1750 | 2000 | 3000 | 4000 |
Three parameters are necessary for Parallel Analysis, the number of variables involved, and the sample size of the research data
the results will be used to compare with. Finally the number of replications.
The number of iterations will determine the stability of the results. Generally, decisions are made using Eigen values to
2 decimal places, and to be stable at this level, about 500 replications are needed.
Most of the results are background. The results used for comparison with Eigen values from research data are
those in the last column, the 95 percentile values.
There is no constraints on the size of the data, as most lap tops will have sufficient memory to cope with matrices of
more than 100 variables.
However, there are constraints related to time required for computation. The more commonly used browsers
(Explorer, Firefox) imposes limits, either in the number of calculations, or amounts of time. When the limit is reached,
the browser ask the user whether he/she wishes to continue. This means, with prolonged computation, the user cannot
leave the computer to do other things, but needs to nurse the program to its conclusions. For example, the Firefox
browser will pause and ask users whether to continue every 10 seconds of computing, and sometimes this becomes tedious
when computation may require several minutes.
The R program takes 3 parameters
- nc is sample size and in this example is 25 cases or rows of data
- nv is the number of variables and in this example is 6
- ni is the number of iterations. In most cases this is between 50 and 1000, and in this example set at 100
The program then calculate the eigen values vector using normally distributed random values (nc rows by nv columns). This is carried out ni times, and the values are stored in vectors of Σx and Σx 2. From these the mean and Standard Deviations are calculated.
The final results are the 95 percentile of these values, which can then be used as the standard to determine the number of factors to retain
# parameters
nc = 25 # nc = number of cases, sample size
nv = 6 # nv = number of variabes
ni = 100 # ni = number of iterations in Monte Carlo simulation
# parallel analysis begin
exVect <- rep(0, nv) # null vector for Σx
exxVect <- rep(0, nv) # null vector for Σx2
for(i in 1:ni) # interate ni times
{
dMx <- replicate(nv, rnorm(nc)) # create matrix of normally distributed random numbers
evVect <- eigen(cor(dMx))$values # vector of eigen values
for(j in 1:nv) # add to vectors of sum x ans sum x sq
{
exVect[j] = exVect[j] + evVect[j]
exxVect[j] = exxVect[j] + evVect[j]^2
}
} # end of interation
resVect <- rep(0,nv) # result vector containing 95 percentile eigen values
for(j in 1:nv)
{
mean = exVect[j] / ni # mean = Σx/n
sd = sqrt((exxVect[j] - exVect[j]^2/ni)/(ni-1)) # Standard Deviation
lim = mean + qnorm(0.95) * sd # 95 percentile limit
resVect[j] = lim
}
print(resVect) # array of 95 percentile eigen values
The results are
[1] 1.9605460 1.5193420 1.2037633 1.0112186 0.7737773 0.5794345
Please note that the values will be slightly different for each calculation, as different random numbers are used. However the differences would be smaller if the number of iterations increases.
|

