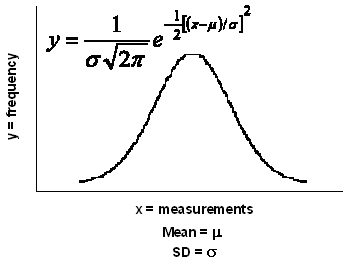 | Content Disclaimer Copyright @2020. All Rights Reserved. |
StatsToDo: Probability of z (Z Test)
Links : Home Index (Subjects) Contact StatsToDo
|
Introduction
The ancient Phoenicians were great traders and sea farers, but they tended to
overload their boats. In stormy weather, goods had to be thrown overboard in
order to save the ship. Owners of lost goods were then compensated by those who
did not lose their goods, and the amounts involved depended on the total value
of the goods. This arrangement was named havara, and this term evolved over the
centuries to become average, and from average the mathematical term mean developed.
Javascript Program
The astronomer, Gauss, measured distances between stars. He noticed that it
was difficult to reproduce his measurements exactly. However, the measurements
clustered around a central value, more common near the mean, and becoming less
common as they are further away from the mean (fig. left).
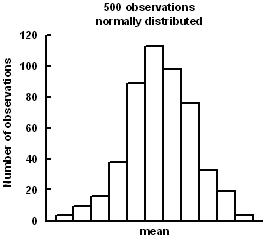
He concluded that any set of measurements would normally distribute to this pattern and called it the Normal Distribution. De Moivre derived the formula for the Normal Distribution curve in
mathematical terms (fig. right).
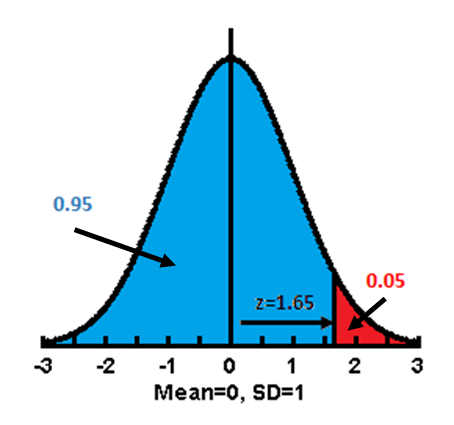
Once this was done, the features of Normal Distribution could be mathematically handled. Using simple calculus, the area under the curve (or any part of it) can be estimated. Fisher developed the concept further and used the area under the curve as a measure of probability. He argues that if the area under the whole curve be consider totality, then any portion represents the probability of the events that describe the portion. From this, he was able to calculate the probability of obtaining a measurement that exceeds a deviation from the mean value. He standardized the measurement of this deviation and called it the Normal Standard Deviate (z), later abbreviated to Standard Deviation, and derived the relationships between z and probability. The other panels of this page are
References
https://en.wikipedia.org/wiki/Standard_normal_table Wikipedia explanation and tables Javascript algorithm adapted from Abramowitz M and Stegun IA (1972) Handbook of mathematical functions. Dover Publications, Inc. New York. Library of Congress Catalog card number 65-12253. p.925
Calculation are presented in maroon and results produced presented in navy
Tables for Probability of z
R CodeProbability of z
ZToP<-function(z) #function to calculate probability from z
{
return (1-pnorm(z))
}
ZToP(1.65) # testing
0.04947147
PToZ<-function(p) #function to calculate z from probability
{
return (-qnorm(p))
}
PToZ(0.05) # testing
1.644854 Python CodeHeader and Library import scipy.stats as stProbability of z
def ZToP(z):
""" Calculate probability from z """
return 1 - st.norm.cdf(z)
print(ZToP(1.64)) # testing
0.050502583474103746
def PToZ(p):
""" Calculate z from probability """
return st.norm.ppf(1 - p)
print(PToZ(0.05)) # testing
1.6448536269514722 Table of frequently used probability and z values
Table of Probability for z The z value is the sum of the first row and first column, and probability is the cell of that row and column. for example, probability=0.40905 when z=0.23 Please be reminded that, although probabilities of z are presented to 5 decimal points of precision in the table, the 2 decimal point precisions are more commonly used.
|
